Nomogram (nomograf): Definition, historie og grafiske beregninger
Lær nomogrammers historie, opbygning og grafiske beregninger — fra d'Ocagnes opfindelse til praktiske eksempler og moderne anvendelser.
Et nomogram, et justeringsdiagram eller et abaque er en grafisk hjælp til beregning. Det er et todimensionelt diagram, der viser en beregning af en matematisk funktion ved hjælp af et sæt skalaer placeret i forhold til hinanden, så kendte værdier giver den ukendte værdi direkte ved aflæsning.
Nomografien blev opfundet i 1884 af den franske ingeniør Philbert Maurice d'Ocagne (1862–1938). Han udviklede metoder til at repræsentere algebraiske sammenhænge grafisk og populariserede brugen af parallelt opstillede skalaer til beregninger. Nomogrammer blev i mange år brugt af ingeniører, teknikere og praktikere til hurtige, feltvenlige beregninger af komplicerede formler uden hjælp af lommeregner eller tabelopslag.
Opbygning og princippet bag
Et nomogram består typisk af et sæt af n skalaer — én skala for hver variabel i en ligning. Ved at kende værdierne af n−1 variabler kan værdien af den ukendte variabel findes visuelt. Resultatet fås ved at lægge et lineal hen over de kendte værdier på skalaerne og aflæse den ukendte værdi dér, hvor linealen krydser skalaen for den pågældende variabel. Den virtuelle eller tegnede linje, der skabes af linealen, kaldes en indekslinje eller en isopleth.
Typer af nomogrammer
- Lineære nomogrammer — skalaerne er lineære; ofte brugt til simple additivt sammenhængende størrelser.
- Logaritmiske nomogrammer — skalaerne er logaritmiske og egner sig godt til multiplicative sammenhænge (fx a·b=c) eller store værdiområder.
- Tre-punkts (og flerpunkts) nomogrammer — standardlayout med tre skalaer, hvor to kendte værdier giver den tredje.
- Cirkulære og polære nomogrammer — skalaer arrangeret rundt om et centrum, nyttigt når rumlige eller vinkelforhold indgår.
- Særlige diagrammer — fx nogle varianter ligner Smith-diagrammer eller andre specialværktøjer inden for elektroteknik og radioteknik.
Konstruktion — hvordan et nomogram laves
- Omskriv først problemets ligning, så den kan repræsenteres grafisk (fx ved at tage logaritmer ved multiplicative forhold eller ved at bruge transformationer, der giver lineære relationer mellem skalaerne).
- Fastlæg de ønskede værdiintervaller for hver variabel og vælg passende skalaform (lineær eller logaritmisk).
- Bestem skalaernes placering og orientering, så en lige linje gennem kendte punkter går gennem det ukendte punkts skala (dette kan kræve algebraisk/geometrisk konstruktion eller numerisk beregning ved designfasen).
- Marker tikker og tal, og kontroller nøjagtigheden ved eksempeleksempler.
En kort illustration (enkelt eksempel)
For en simpel multiplicativ sammenhæng a·b = c kan man bruge logaritmiske skalaer for a, b og c. Når log(a) og log(b) aflæses på hver sin skala, vil en lineal tværs over disse to punkter krydse skalaen for log(c) i punktet svarende til log(a) + log(b), hvilket giver c ved anti-logaritme. Det er netop denne egenskab ved log-skalaer, der gør nomogrammer praktiske til multiplikation og division.
Anvendelser
- Teknik og ingeniørarbejde — hurtige feltberegninger, dimensionering og kontrol.
- Medicin — doseringsdiagrammer og prognoseværktøjer (fx nogle klassiske medicinske nomogrammer til risikovurdering).
- Geologi, hydrologi og meteorologi — omregninger og tabeller integreret i ét diagram.
- Militær og navigation — feltudstyr der kræver hurtige, robuste beregninger uden elektronisk udstyr.
- Undervisning — visualisering af funktionssammenhænge og logiske transformationer.
Fordele og begrænsninger
- Fordele: hurtig aflæsning i marken, intuitiv visuel forståelse af sammenhænge, ingen strøm eller computere nødvendig, nyttig til undervisning og demonstration.
- Begrænsninger: begrænset præcision sammenlignet med digitale beregninger (afhængig af skalernes opløsning og aflæsningsteknik), kan blive kompliceret ved mange variabler eller ikke-monotone funktioner, og selve konstruktionsfasen kan være matematisk krævende.
Moderne status
Med udbredelsen af regnemaskiner og software faldt den praktiske brug af nomogrammer i slutningen af 1900-tallet, men de lever videre i specialområder og som pædagogisk værktøj. I dag findes der digitale værktøjer og webbaserede generatorer til at designe nomogrammer, og fagfolk bruger dem stadig, når hurtig, visuel beregning eller robust feltmetode er ønsket.
Praktiske tips til brug
- Brug en tynd lineal eller et transparent lineal for at minimere parallaxefejl ved aflæsning.
- Tjek nomogrammets validitetsområde (værdier uden for bestemte intervaller kan give forkerte resultater).
- Kalibrer og test nomogrammet mod kendte eksempler for at vurdere nøjagtigheden.
Nomogrammer repræsenterer et elegant matematisk-håndværksmæssigt kompromis mellem algebraisk præcision og praktisk anvendelighed — et simpelt, visuelt værktøj med rødder i 1800-tallets ingeniørarbejde, som stadig har plads i moderne fagpraksis og undervisning.
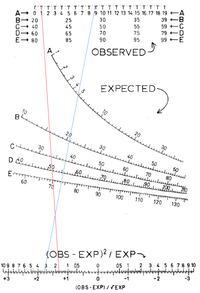
Nomogram for chi-kvadratfordeling
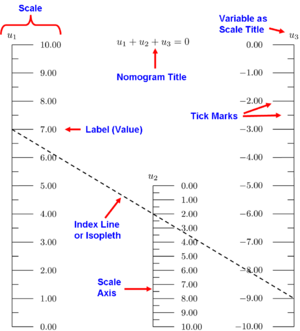
Komponenter i et nomogram i parallelskala
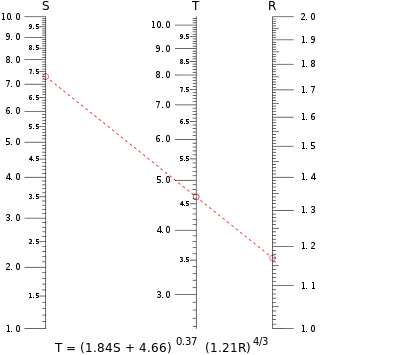
Et typisk nomogram i parallelskala. I dette eksempel beregnes værdien af T, når S = 7,30 og R = 1,17 indsættes i ligningen. Isopletten krydser skalaen for T ved lige under 4,65.
Brug
Nomogrammer blev anvendt i ca. 75 år i stor stil. De gjorde det muligt at foretage hurtige og nøjagtige beregninger før lommeregnernes tid. Resultaterne fra et nomogram fås hurtigt og pålideligt ved at tegne en eller flere linjer. Brugeren behøver ikke at vide, hvordan man løser algebraiske ligninger, slår data op i tabeller, bruger en regnestok eller indsætter tal i ligninger for at få resultater. Brugeren behøver ikke engang at kende den underliggende ligning, som nomogrammet repræsenterer.
Nomogrammer har domæneviden i deres udformning. For at skabe større nomogrammer med henblik på større nøjagtighed medtager nomografen f.eks. normalt kun skalaområder, der er rimelige og af interesse for problemet. Mange nomogrammer indeholder andre nyttige markeringer som f.eks. referencemærker og farvede områder. Alle disse giver brugeren nyttige rettesnore.
Ligesom en regnestok er et nomogram en grafisk analog beregningsanordning. Ligesom regnestokken er dens nøjagtighed begrænset af den præcision, hvormed fysiske markeringer kan tegnes, reproduceres, ses og justeres.En regnestok er en regnemaskine til generelle formål, men et nomogram er designet til at udføre en specifik beregning. Nomogrammer kan stadig bruges til at kontrollere et svar fra en anden, mere nøjagtig, men muligvis fejlbehæftet beregning.
Spørgsmål og svar
Q: Hvad er et nomogram?
A: Et nomogram er en graf, der bruges til beregning, og som giver en beregning af en matematisk funktion.
Q: Hvem opfandt nomografien?
A: Nomografi blev opfundet af Philbert Maurice d'Ocagne, en fransk ingeniør, i 1884.
Q: Hvad var formålet med nomogrammer?
A: Nomogrammer blev brugt i mange år til at give ingeniører hurtige grafiske beregninger af komplicerede formler.
Q: Hvor mange skalaer består et nomogram af?
A: Et nomogram består af et sæt af n skalaer, en for hver variabel i en ligning.
Q: Hvordan kan man finde værdien af en ukendt variabel ved hjælp af et nomogram?
A: Når man kender værdierne af n-1 variable, kan man finde værdien af den ukendte variabel ved at lægge en lineal hen over de kendte værdier på skalaerne og aflæse den ukendte værdi der, hvor den krydser skalaen for den pågældende variabel.
Q: Hvad kaldes den virtuelle eller tegnede linje, der skabes af linealen?
A: Den virtuelle eller tegnede linje, der skabes af linealen, kaldes en indekslinje eller isoplet.
Q: Hvilken slags koordinatsystem bruges i nomogrammer?
A: Nomogrammer bruger et parallelt koordinatsystem opfundet af d'Ocagne i stedet for standard kartesiske koordinater.
Søge