Normalkraft: Hvad er det? Definition, formel og eksempler
Forstå normalkraft: definition, formel (mg, mg·cosθ), tydelige eksempler og anvendelser på flade og skrå planer — klar guide til studerende og teknikere.
Normalkraften er den kraft, som jorden (eller en hvilken som helst overflade) skubber tilbage opad med. Hvis der ikke var nogen normalkraft, ville du langsomt sive ned i jorden.
Den normale kraft på et objekt er altid vinkelret på den overflade, som objektet befinder sig på.
På en flad overflade er normalstyrken på et objekt m g {\displaystyle mg} 
(genstandens vægt, dvs. dens masse multipliceret med tyngdekraften).
På et skråt plan reduceres normalkraften med vinklen, og normalkraften er m g c o s θ {\displaystyle mgcos\theta } 
.
Bemærk, at på en flad overflade 
ville θ {\displaystyle \theta } være 0, og derfor ville c o s θ {\displaystyle cos\theta }
være 1. De to ligninger er således lige store.
Hvad er normalkraften præcist?
Normalkraften er den kontaktkraft en overflade udøver på et legeme for at forhindre, at legemet trænger igennem overfladen. Den er altid rettet vinkelret (normal) på kontaktfladen. Ifølge Newtons tredje lov er normalkraften reaktion på den kraft, som legemet trykker mod overfladen med.
Formler og hvordan man får dem
- På en horisontal (flad) overflade: N = mg, hvor m er massen og g er tyngdeaccelerationen (typisk ≈ 9,81 m/s²).
- På et skråplan med vinkel θ (målt mellem planet og den vandrette): N = mg cos θ. Her er tyngdekraftens komponent vinkelret på planet mg cos θ, som balanceres af normalkraften.
Forklaring: Tyngdekraften mg peger lodret ned. Når et objekt ligger på et skråt plan deles mg op i to komponenter: mg cos θ vinkelret på planet (giver normalkraften) og mg sin θ parallelt med planet (giver en tendens til at glide ned ad planet).
Eksempler
- Eksempel — skråplan: Et objekt med m = 5,00 kg ligger på et plan med θ = 30°. Normalkraften bliver N = m g cos θ ≈ 5·9,81·cos30° ≈ 42,5 N.
- Eksempel — elevator: Hvis en person på 70 kg står i en elevator, der accelererer opad med a = 2,00 m/s², bliver normal- (dvs. "apparent weight") N = m(g + a) ≈ 70·(9,81+2,00) ≈ 827 N. Hvis elevatoren i stedet accelererer nedad, trækkes N = m(g − a). Ved frit fald (a = g) er N = 0 — man er vægtløs i forhold til elevatorens bund.
Vigtige bemærkninger og anvendelser
- Retning: Normalkraften ændrer altid retning i takt med overfladens orientering. På en buet overflade ændres normalens retning langs bevægelsen.
- Ikke altid lig mg: N er kun lig mg hvis der ikke er andre lodrette kræfter og hvis systemet ikke accelererer lodret. Ved lodret acceleration ændres N.
- Forbindelse til friktion: Coulombs friktion er proportional med normalkraften: F_f ≤ μN, hvor μ er friktionskoefficienten. På et skråplan er maksimal statisk friktion typisk μ_s mg cos θ.
- Kontakt og deformation: Normalkraften kommer fra mikroskopiske deformationer i kontaktflader. Selvom overfladen ser stiv ud, deformeres materialet en smule, hvilket skaber den opadrettede reaktionskraft.
Tips til fri-kraftsdiagrammer
- Start med at tegne alle kræfter: tyngdekraft (mg) nedad, normal (N) vinkelret på fladen, evt. friktion langs fladen, og andre ydre kræfter.
- Opdel mg i komponenter parallelt og vinkelret på planet: mg cos θ (vinkelret) og mg sin θ (parallelt).
- Brug Newtons 2. lov i hver retning for at finde N, acceleration eller friktionskræfter.
Sammenfatning
Normalkraften er den kontaktkraft, der virker vinkelret på en overflade og forhindrer, at et objekt trænger igennem denne overflade. På en flad horisontal overflade er N normalt lig med vægten mg, mens N på et skråt plan er mg cos θ. Normalkraften er central for forståelsen af friktion, bevægelse på hældninger og "apparent weight" i accelererende systemer.
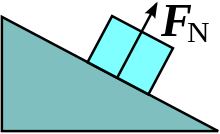
FN repræsenterer normalkraften
Spørgsmål og svar
Q: Hvad er normalkraft?
A: Normalkraft er den kraft, som jorden (eller en hvilken som helst overflade) skubber tilbage opad med.
Q: Hvad ville der ske, hvis der ikke var nogen normalkraft?
A: Hvis der ikke var nogen normalkraft, ville du langsomt sive ned i jorden.
Spørgsmål: Hvordan hænger normalkraften på en genstand sammen med dens vægt?
A: På en flad overflade er normalkraften på en genstand lig med dens vægt (genstandens masse ganget med tyngdekraften).
Spørgsmål: Hvordan påvirker et skråplan normalstyrken?
A: På et skråt plan reduceres normalkraften med vinklen, og den kan beregnes ved hjælp af m g c o s θ.
Spørgsmål: Hvad repræsenterer θ i denne ligning?
A: θ repræsenterer hældningsvinklen i denne ligning.
Spørgsmål: Hvornår vil cosθ være 1?
Svar: cosθ vil være 1, når θ (vinkel)er 0, hvilket sker på en flad overflade.
Spørgsmål: Hvordan kan disse to ligninger sammenlignes med hinanden? Svar: De to ligninger er lige store, når de er på en flad overflade.
Søge