Hollands skema-sætning: Definition og betydning for genetiske algoritmer

Hollands skema-sætning: klar definition og betydning for genetiske algoritmer — forstå skemaer, evolutionær dynamik og implikationer for GA-ydeevne.

Forfatter: Leandro Alegsa

05-03-2026 15:54

Hollands skema-sætning, også kaldet den grundlæggende sætning for genetiske algoritmer, er en ulighed, der følger af en grovkornet ligning for evolutionær dynamik. Skema-teoremet siger i sin enkleste form, at korte, lave skemaer med en fitness over gennemsnittet øges i hyppighed i successive generationer, typisk eksponentielt når betingelserne er gunstige. Sætningen blev foreslået af John Holland i 1970'erne og blev i første omgang bredt opfattet som grundlaget for forklaringer på de genetiske algoritmers styrke. Denne fortolkning er dog blevet nuanceret og kritiseret i senere arbejde, hvor man bl.a. viser, at skema-teoremet kan betragtes som et specialtilfælde af Price-ligningen med skemaindikatorfunktionen som den makroskopiske måling.

Et skema er en skabelon, der identificerer en delmængde af strenge ved at spesificere værdier på nogle positioner og lade andre positioner være vilkårlige (ofte skrevet med et wildcard-symbol, fx “*”). Eksempel: skemaet 1*0*1 matcher alle bitstrenge af længde 5, hvor positionerne 1, 3 og 5 er hhv. 1, 0 og 1, mens positionerne 2 og 4 kan være enten 0 eller 1. Skemaer er et specialtilfælde af cylindermængder og udgør derfor et topologisk rum, hvilket gør det muligt at betragte algebraiske og måltekniske egenskaber ved udvalg af skemaer.

Formelt indhold og notation

Nogle centrale begreber og notation, som Holland brugte:

o(H) — skemaets orden: antallet af faste positioner (ikke-wildcards) i skemaet H.
δ(H) — skemaets definerende længde: afstand mellem skemaets første og sidste faste position.
m(H,t) — antal (eller andel) individer i populationen ved generation t, der matcher skemaet H.
f(H) — gennemsnitlig fitness blandt alle individer, der matcher H; f̄ er den gennemsnitlige fitness i hele populationen.
p_c — sandsynlighed for crossover; p_m — sandsynlighed for mutation per bit.

Den klassiske skema-ulikhed (et nedre bound) kan formuleres (i en forenklet form) som en forventning for antallet af skema-eksemplarer i næste generation:

E[m(H,t+1)] ≥ m(H,t) · (f(H)/f̄) · (1 − p_c · δ(H)/(l−1) − o(H) · p_m)

Her er l længden af hele strengen. Læseren bør bemærke, at denne formel er en forenkling og giver et konservativt estimat: den antager, at crossover og mutation kun kan ødelægge skemaet (disruptive effekter) og medregner ikke muligheder for, at de samme operationer kan skabe nye forekomster af H.

Intuition og implikationer

Essensen af teoremet er, at kortfattede (lave δ) og lave-ordens (lave o) skemaer, som har højere end gennemsnitsfitness, tenderer til at blive overrepræsenteret i efterfølgende generationer. Dette gav grobund for den såkaldte building-block hypothesis: at genetiske algoritmer samler og kombinerer små, fordelagtige byggesten (skemaer) for gradvist at konstruere bedre løsninger.

Begrænsninger og kritik

Skema-teoremet giver et nedre bound (en ulighed), ikke en eksakt evolutionær ligning; derfor er det ikke et fuldstændigt prædiktionsværktøj for GA-adfærd i praksis.
Formlen overser ofte skabelsesmekanismer: crossover og mutation kan både ødelægge og skabe skemaer, så et rent fokus på "bevarelse" er ufuldstændigt.
Teoremet fremsætter ikke, og kan ikke bevise, at GAs altid er effektive — deres succes afhænger af problemets landskab, repræsentation, parametervalg og populationens mangfoldighed.
Som nævnt ovenfor kan skema-teoremet udledes fra mere generelle rammer som Price-ligningen ved at vælge skemaets indikatorfunktion som måling; dette viser, at teoremet er en matematisk konsekvens af bredere evolutionære principper og ikke i sig selv en komplet forklaring på GAers effektivitet.

Praktiske konsekvenser for design af genetiske algoritmer

Repræsentation: Kortere definerende længder for vigtige byggesten og kodningsvalg, der samler relevante variable tættere, reducerer sandsynligheden for ødelæggelse ved crossover.
Parametervalg: Moderat crossover-sandsynlighed og lave mutationrater mindsker destruktion af små byggesten, men man må sikre tilstrækkelig mutation/variation for at opdage nye gode skemaer.
Population og selektion: Tilstrækkelig stor population og passende selektionsstyrke bevarer mangfoldighed, så lovende skemaer ikke tabes tidligt.
Rekombinationsoperatorer: Problemtilpassede crossover- og mutationsoperatorer kan reducere uheldig fragmentering af værdifulde skemaer og nogle gange aktivt genoprette dem.

Sammenfattende er Hollands skema-sætning et vigtigt teoretisk værktøj til at forstå nogle grundlæggende mekanismer i genetiske algoritmer: hvordan små fordelagtige mønstre kan forstærkes over tid. Den skal dog anvendes med omtanke og suppleres af bredere analyser (fx Price-ligning, empiriske eksperimenter og landskabsanalyser) for fuldt ud at beskrive og forudsige en GAs opførsel i konkrete problemer.

Beskrivelse

Betragt binære strenge af længde 6. Skemaet 1*10*1 beskriver mængden af alle strenge af længde 6 med 1'er på positionerne 1, 3 og 6 og et 0 på position 4. * er et wildcard-symbol, hvilket betyder, at positionerne 2 og 5 kan have værdien 1 eller 0. Ordningen af et skema o ( H ) {\displaystyle o(H)} $o(H)$ er defineret som antallet af faste positioner i skabelonen, mens den definerende længde δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ er afstanden mellem den første og den sidste specifikke position. Ordningen af 1*10*1 er 4, og den definerende længde er 5. Et skemas egnethed er den gennemsnitlige egnethed af alle strenge, der passer til skemaet. En strengs egnethed er et mål for værdien af den kodede problemløsning, som beregnes af en problemspecifik evalueringsfunktion. Ved hjælp af de etablerede metoder og genetiske operatører i genetiske algoritmer fastslår skema-sætningen, at korte, lavtordnede skemaer med en fitness over gennemsnittet stiger eksponentielt i de efterfølgende generationer. Udtrykt som en ligning:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Her er m ( H , t ) {\displaystyle m(H,t)} $m(H,t)$ antallet af strenge, der tilhører skema H {\displaystyle H} $H$ ved generation t {\displaystyle t} $t$ , f ( H ) {\displaystyle f(H)} $f(H)$ er den observerede gennemsnitlige fitness for skema H {\displaystyle H} $H$ og a t {\displaystyle a_{t}} $a_{t}$ er den observerede gennemsnitlige fitness ved generation t {\displaystyle t} $t$ . Sandsynligheden for forstyrrelse p {\displaystyle p} $p$ er sandsynligheden for, at krydsning eller mutation vil ødelægge skemaet H {\displaystyle H} $H$ . Den kan udtrykkes som:

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

hvor o ( H ) {\displaystyle o(H)} $o(H)$ er rækkefølgen af skemaet, l {\displaystyle l} $l$ er kodens længde, p m {\displaystyle p_{m}} $p_{m}$ er sandsynligheden for mutation og p c {\displaystyle p_{c}} $p_{c}$ er sandsynligheden for crossover. Så et skema med en kortere definerende længde δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ er mindre tilbøjeligt til at blive forstyrret.
Et ofte misforstået punkt er, hvorfor skema-sætningen er en ulighed snarere end en lighed. Svaret er faktisk enkelt: Sætningen negligerer den lille, men ikke-nul, sandsynlighed for, at en streng, der tilhører skemaet H {\displaystyle H} $H$ , vil blive skabt "fra bunden" ved mutation af en enkelt streng (eller rekombination af to strenge), der ikke tilhørte H {\displaystyle H} $H$ i den foregående generation.

Begrænsning

Teoremet om skemaer gælder under forudsætning af en genetisk algoritme, der opretholder en uendelig stor population, men det overføres ikke altid til (endelig) praksis: på grund af fejl i den oprindelige population kan genetiske algoritmer konvergere mod skemaer, der ikke har nogen selektiv fordel. Dette sker især i multimodal optimering, hvor en funktion kan have flere toppe: populationen kan drive til at foretrække en af toppene og ignorere de andre.

Grunden til, at skemateoremet ikke kan forklare de genetiske algoritmers styrke, er, at det gælder for alle probleminstanser og ikke kan skelne mellem problemer, hvor genetiske algoritmer klarer sig dårligt, og problemer, hvor genetiske algoritmer klarer sig godt.

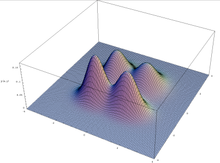
Plot af en multimodal funktion i to variabler.

Spørgsmål og svar

Spørgsmål: Hvad er Hollands skemateorem?

Svar: Hollands skemateorem er et teorem vedrørende genetiske algoritmer, der siger, at individer med en fitness, der er højere end gennemsnittet, har større sandsynlighed for at sejre.

Sp: Hvem foreslog Hollands skema-sætning og hvornår?

Svar: John Holland foreslog Holland's skema-sætning i 1970'erne.

Spørgsmål: Hvad er et skema i forbindelse med genetiske algoritmer?

Svar: I forbindelse med genetiske algoritmer er et skema en skabelon, der identificerer en delmængde af strenge med ligheder på bestemte strengepositioner.

Spørgsmål: Hvordan fortolkes Hollands skemateorem, der blev brugt som grundlag for forklaringer på de genetiske algoritmers styrke?

Svar: Fortolkningen af Hollands skemateorem, der blev brugt som grundlag for forklaringer på de genetiske algoritmers styrke, er, at individer med en fitness, der er højere end gennemsnittet, har større sandsynlighed for at sejre.

Spørgsmål: Hvad har kritikken af Hollands skemateorem vist, at den er?

Svar: Kritikken af Hollands skema-sætning har vist, at den er et specialtilfælde af Price-ligningen med skemaindikatorfunktionen som makroskopisk målestok.

Spørgsmål: Hvad er et specialtilfælde af cylindermængder?

Svar: Skemaer er et specialtilfælde af cylindermængder.

Spørgsmål: Hvilken slags rum danner skemaer?

A: Skemata danner et topologisk rum.

Søge