Det kinesiske tonesystem: 12-lü, kvinter og pentatoniske skalaer

Udforsk det kinesiske tonesystem: 12-lü, kvinter og pentatoniske skalaer — historisk matematik, instrumentbygning og forklaring af de 144 frekvenser på en klar, praktisk måde.

Det gamle kinesiske musiksystem er baseret på enkle, men gamle matematiske principper, som bruges til at bestemme tonernes frekvenser. En god måde at forstå systemet på er at gennemgå et konkret, praktisk eksempel — både for at se beregningerne og for at forstå idéen bag de såkaldte 12‑lü (十二律).

Bygning af et instrument efter 12‑lü‑princippet

Forestil dig, at du vil lave et simpelt strengeinstrument, som kan afspille de toner, der fremkommer i det gamle kinesiske system. Her er en vejledning, der viser princippet:

• Lav en trækasse, fx 105 cm lang og 60 cm bred. Fastgør styrer til snorene i hver ende, så de to styrer er 99 cm fra hinanden. (99 cm er blot et valgt udgangspunkt — længden bestemmer en grundtone.)
• Forholdet mellem strenglængde og frekvens er omvendt: hvis en strenglængde ganges med 2/3, vil frekvensen blive 3/2 gange større (en kvint højere). Derfor kan man få kvinter ved at placere bånd på de steder, hvor længden er 2/3 af en tidligere længde.
• Start med 99 cm. Multiplicer 99 med 2/3 → 66 cm. Sæt et bånd ved 66 cm (det giver en kvint over grundtonen).
• Multiplicer 66 cm med 4/3 → 88 cm, og sæt et bånd der. (Her svarer 88 cm til en anden tone i kredsen, fordi 66·4/3 = 88; længderne flytter sig rundt i oktavområdet.)
• Fortsæt ved at multiplicere skiftevis med 2/3 og 4/3: 88·2/3 ≈ 58,666… cm, 58,666…·4/3 ≈ 78,222… cm, 78,222…·2/3 ≈ 52,148… cm osv. Sæt bånd ved hver af disse længder.
• Når en beregnet længde bliver for kort i forhold til dit ønskede register, kan du fordoble den (dvs. flytte en oktav op eller ned) så den passer ind i samme oktavmæssige område som de andre bånd (fx 46,354 → 92,708 cm ved fordobling).
• Fortsæt processen, indtil du har markeret 11 steder plus den åbne streng — det giver i alt 12 bestemte positioner pr. streng (deraf navnet 12‑lü).

Forklaringen på, hvorfor man skifter mellem 2/3 og 4/3, er knyttet til, at man danner en række af kvinter (forholdet 3:2). Når man ganger med 3/2 i frekvensdomænet svarer det til at gange med 2/3 i længde; hvis længden bliver for lille, flytter man tonen en oktav (ganger med 2 i længde eller deler frekvensen med 2) for at holde den i samme registreringsområde. Den gentagne anvendelse af kvinter og octavekorrigering skaber de 12 forskellige grundtoner i systemet.

Fra bånd til frekvenser og antallet af toner

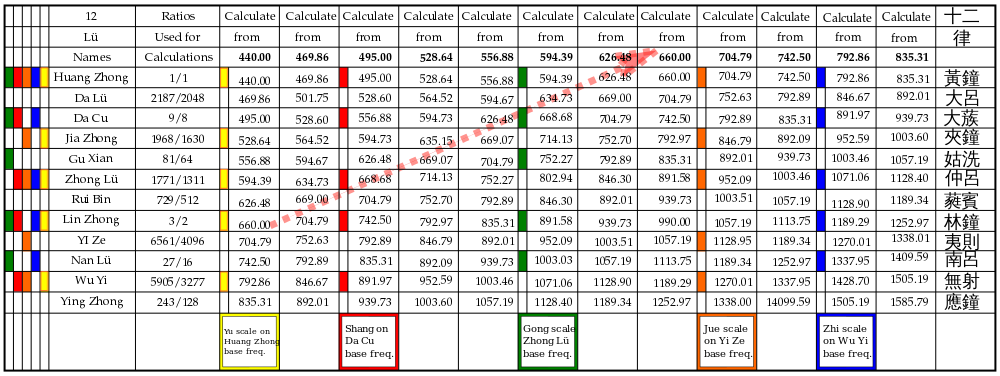
Hvis du tæller frekvensen på den åbne streng og frekvenserne ved de båndede positioner, får du for hver streng 12 definerede frekvenser (12‑lü). Hvis du lader hver streng stemme til en af de 12 positioner som grundtone og har tolv strenge stemt til hver sin af de 12 grundtoner, får du teoretisk op til 144 forskellige toner (12 × 12). Mange af disse vil være oktavlige eller nære dubletter, men fordi forholdene ikke er det samme som i den europæiske lige-tempererede skala, vil der være flere små forskelle i intervalstørrelser og færre nøjagtige gentagelser end i lige temperering.

Matematikkens kerne: kvinter og oktaver

Det centrale i systemet er byggestenene:

• Kvint — forholdet 3:2 (i længde: 2/3). Giver den velkendte musikalske kvint.
• Oktav — forholdet 2:1 (i længde: 1/2). Når en tone flyttes en oktav, fordobles eller halveres frekvensen.

Ved gentagne kvinter og efterfølgende oktavkorrigeringer opnår man en kreds af tolv toner, som ikke er lige fordelt som i moderne ligetemperering, men som følger de rene rationelle forhold (juste intervaller) udledt af kvintkæden.

Skalaer: pentatoniske og heptatoniske

Ud af hver tolvtoneskreds kan man danne forskellige skalaer. De mest karakteristiske i kinesisk tradition er pentatoniske skalaer (fem toner): man vælger fem toner fra de tolv, typisk sådan at ingen af de valgte toner er naboer i 12‑lü‑kredsen — det undgår halvtone‑trin og giver den åbne, «pentatoniske» klang, som vi ofte forbinder med traditionel kinesisk musik. Traditionelt taler man om fem grundlæggende pentatoniske modaliteter (navneoversættelser fra kinesisk): 宫 (gōng), 商 (shāng), 角 (jué), 徵 (zhǐ), 羽 (yǔ). Hver af disse fungerer som et centralt tonecenter (ligesom «tonika» i vestlig musik) og kan danne grundlag for melodier.

Man kan også bygge heptatoniske (syvtonede) skalaer ud af 12‑lü, men disse heptatoniske systemer i traditionel kinesisk musik er ikke identiske med vestlige dur‑ og molsystemer. I Vesten lærer mange elever den syvtonede durskala med navnene «do, re, mi, fa, sol, la og ti» — disse syv udgør en durskala, og vi bruger også ofte en molskala i vestlig musik. Kinesisk musik hviler oftere på de femtonige pentatoniske modaliteter end på en entydig dur/mol‑deling.

Historisk baggrund

Idéen om at skabe en kreds af tolv tonesteder går langt tilbage i kinesisk teori. Den klassiske fremstilling af 12‑lü (十二律) blev systematiseret af bl.a. teoretikere som Jing Fang (京房) i Han‑perioden, som udnyttede kvintkæden til at beregne konsonante intervalforhold. Metoden er uafhængig af nutidens lige-tempererede system og bygger i stedet på rationelle brøker (just intonation), som giver nogle meget rene intervaller, men også nogle uundgåelige uoverensstemmelser (enharmoniiske forskelle), når man vil lukke kredsen efter tolv kvinter.

Praktiske kommentarer

• De numeriske eksempler (fx startlængde 99 cm) er tænkt som et illustrativt byggeprojekt. I praksis vælges grundfrekvenser efter ønsket tonehøjde (fx en A på 440 hertz), og så multipliceres denne grundfrekvens med passende forholdstal for at få de andre toner.
• Hver af de 12 frekvenser kan bruges som udgangspunkt for en kolonne af toner — og derfra kan man plukke fem toner til en pentatonisk skala, så længe de ikke ligger lige ved siden af hinanden i kredsen (dvs. undgår halvtonetrin og derved får den karakteristiske pentatoniske form).
• Systemet giver en rig tonal variation, men også kompleksitet ved modulation (skift mellem tonecentre), fordi intervallerne ikke er ligeligt fordelt som i lige temperering.

Samlet set viser denne metode, hvordan simple multiplikationer og octavekorrigeringer kan skabe et helt tonesystem: 12 faste toner pr. oktav, muligheden for at danne både pentatoniske og heptatoniske skalaer og et musikalsk univers, der adskiller sig fra den vestlige lige-tempererede tradition — både i lyd og i måde at tænke musik på.

Spørgsmål og svar

Spørgsmål: Hvad er det gamle kinesiske musiksystem baseret på?

Q: Hvordan laver man et musikinstrument, der kan spille enhver sang i det gamle kinesiske system?

Spørgsmål: Hvad er et eksempel på en heptatonisk skala?

Spørgsmål: Hvor mange forskellige skalaer bruger traditionel kinesisk musik?

Spørgsmål: Bliver pentatoniske skalaer diskuteret i denne artikel?

Spørgsmål: Hvilken frekvens blev valgt som eksempel?

Spørgsmål: Hvor mange frekvenser vil blive frembragt, når alle tolv strenge plukkes i både båndede og ufrankerede positioner?

Søg efter bogstav